Коэффициент информации менеджера равен 0,75. Определите, какое количество лет необходимо управлять портфелем, чтобы получить результат, подтверждающий способность менеджера управлять портфелем с доверительной вероятностью 95%.
- Рынок ценных бумаг
Условие:
1. В начале года в портфель инвестировали 10 млн.руб. Через три месяца его стоимость выросла до 11 млн.руб., и наследующий день в портфель внесли дополнительно 2 млн.руб. В конце следующего квартала стоимость портфеля составила 12 млн.руб., и из него изъяли 3 млн.руб. Еще через три месяца стоимость портфеля составила 10 млн.руб. и в него добавили 1 млн.руб. В конце года стоимость портфеля составила 12 млн.руб. Определите доходность управления портфелем.
2. В начале года стоимость портфеля составила 500000 руб. Через четыре месяца она выросла до 600000 руб., и из портфеля изъяли 12000 руб. Еще через четыре месяца стоимость портфеля выросла до 612500 руб., и в него добавили 20000 руб. В конце года стоимость портфеля составила 683100 руб. Определите доходность портфеля за год.
3. Средняя ставка без риска за некоторый период равна 15%, средняя доходность первого портфеля - 24%, второго - 21%. Бета первого портфеля - 1,2, второго - 0,8. Оцените эффективность управления этими портфелями на основе показателя Трейнора.
4. Средняя ставка без риска за некоторый период равна 15%, средняя доходность первого портфеля - 24%, второго - 21%. Бета первого портфеля - 1,2, второго - 0,8. Оцените эффективность управления этими портфелями на основе показателя Шарпа.
5. Коэффициент информации менеджера равен 0,75. Определите, какое количество лет необходимо управлять портфелем, чтобы получить результат, подтверждающий способность менеджера управлять портфелем с доверительной вероятностью 95%.
Решение:
1. Доходность портфеля = 11/10*12/(11+2)*10/(12-3)*12/(10+1)-1=23,08%
2.Доходность портфеля = 600000/500000*612500/(500000-12000)*683100/(612500+20000)-1=0,35 или 35%
3.Показатель Трейнора первого портфеля равен: 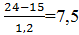 ; второго портфеля:
; второго портфеля:
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства