1. Главная
  2. Библиотека
  3. Сопротивление материалов
  4. Дан стержень площадью F1, длиной 2a на первом и площадью F2, длиной a на втором участке (рисунок 1), нагруженный распредел...

Дан стержень площадью F1, длиной 2a на первом и площадью F2, длиной a на втором участке (рисунок 1), нагруженный распределенной нагрузкой q и сосредоточенной силой P=qa; Е – модуль продольной упругости материала, а F1 = F2 = F.

«Дан стержень площадью F1, длиной 2a на первом и площадью F2, длиной a на втором участке (рисунок 1), нагруженный распределенной нагрузкой q и сосредоточенной силой P=qa; Е – модуль продольной упругости материала, а F1 = F2 = F.»
  • Сопротивление материалов

Условие:

Дан стержень площадью F1, длиной 2a на первом и площадью F2, длиной a на втором участке (рисунок 1), нагруженный распределенной нагрузкой q и сосредоточенной силой P=qa; Е – модуль продольной упругости материала, а F1 = F2 = F.

Требуется построить эпюры распределения продольного усилия N(x) и функции перемещений ∆l(x), а также найти максимальное напряжение σmax.

Исходные данные 

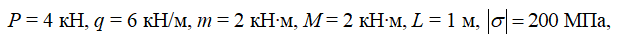
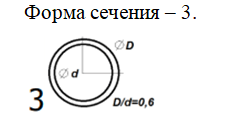
Решение:

Значение а = Р/q = 4/6 = 0.67 м.

Примем F = 5 см2.

1. Определим реакцию в заделке Rx из уравнения равновесия: сумма проекций всех сил на ось x стержня равна нулю. Распределенную нагрузку q на длине 2a приведем к сосредоточенной 2qa:

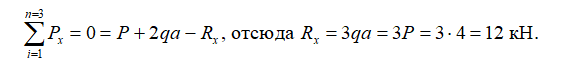
2. Величину реакции Rx проверяем по эпюре усилий N(x).

3. Разобьем стержень на два участка и пронумеруем их. Этот пункт выполнен согласно исходным данным.

4. Применим мет...

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я