Для пунктов в) и г) считать, что в генеральной совокупности значения признака X распределены по нормальному закону и генеральная дисперсия совпадает с исправленной выборочной дисперсией.
- Статистика
Условие:
Дано дискретное статистическое распределение выборочных значений количественного признака X:
а) Вычислить выборочную среднюю, выборочную дисперсию и выборочное среднее квадратическое отклонение признака X
б) Построить полигон относительных частот
в) Указать точечные оценки для генеральных характеристик признака: генеральной средней a, генеральной дисперсии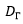 
и генерального среднего квадратического отклонения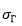 
г) Найти доверительный интервал для генеральной средней с надежностью 99%
Для пунктов в) и г) считать, что в генеральной совокупности значения признака X распределены по нормальному закону и генеральная дисперсия совпадает с исправленной выборочной дисперсией.
Решение:
Объем выборки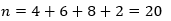 
Выборочную среднюю найдем по формуле:
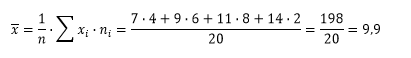
Выборочная дисперсия:
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства