Имеются данные для двадцати вариантов по факторному и результативному признаку относительно времени тренировки и полученных баллов в итоге. Выполнить проверку на однородность и нормальность распределения по факторному признаку.
- Статистика
Условие:
Имеются данные для 20 вариантов по факторному и результативному признаку относительно времени тренировки и полученных баллов в итоге. Выполнить проверку на однородность и нормальность распределения по факторному признаку. Исключить резко выделяющиеся значения из массы первичной информации.
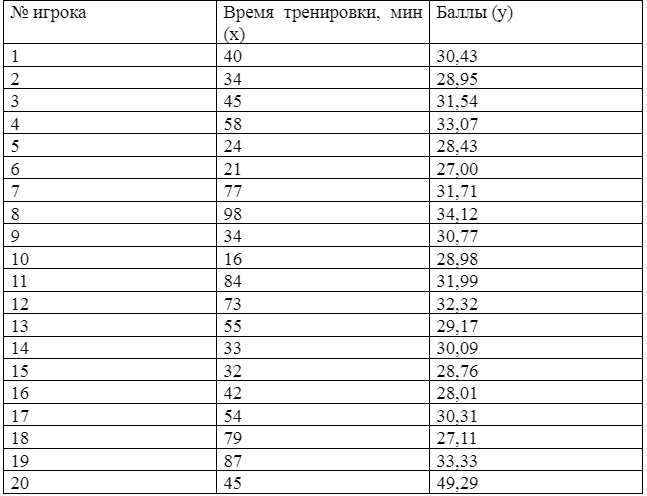
Время тренировки, мин (х) – факторный признак
Баллы – результативный признак
2. Получив однородный массив, выполнить группировку, характеризующую зависимость результативного признака от факторного. Построить ряд распределения с равными интервалами по х, рассчитав величину интервала и число групп по формуле Стерджесса. Определить показатели центра распределения, показатели вариации, асимметрии. Сформулировать выводы.
3.Используя ранее выполненную группировку, проверить правило сложения дисперсий и сделать выводы о степени влияния факторного признака на величину результативного.
4.Выявить факт наличия связи между х и у. определить степень тесноты связи линейного коэффициента корреляции. Анализ выполнить в следующей последовательности:
- установить факт наличия корреляционной зависимости с помощью групповой таблицы и ее направление, дать графическое изображение связи;
- измерить степень тесноты связи с помощью линейного коэффициента корреляции и корреляционного отношения; проверить возможность использования линейной функции в качестве формы уравнения;
- рассчитать параметры уравнения регрессии, оценить его достоверность, используя среднюю квадратическую ошибку. Дать оценку результатов исследования целом.
Решение:
1. Проверка первичной информации на однородность производится с помощью коэффициента вариации. На практике считается, что если этот коэффициент менее 40%, то совокупность однородная.
Коэффициент вариации определим по формуле
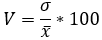
- среднее квадратическое отклонение
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства