Условие задачи
По данным страховых компаний некоторой страны известно, что продолжительность жизни человека есть случайная величина ξ (лет), имеющая показательный закон распределения.
Найти математическое ожидание и среднее квадратическое отклонение этой случайной величины, если известно, что человек доживает до 75 лет с вероятностью 0,2.
Построить схематично графики функции распределения и функции плотности распределения этой случайной величины.
Вычислить вероятность того, что случайно выбранный новорожденный человек проживет:
а) не более 60 лет;
б) не менее 70 лет;
в) от 50 до 80 лет.
г) Какова вероятность прожить до 70 лет клиенту страховой кампании, если ему сейчас 50 лет?
Ответ
Функция распределения экспоненциально распределенной случайной величины с параметром а имеет вид:
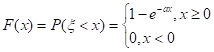
Время жизни по условию измеряется в годах.
Получаем вероятность дожить до 75 лет:
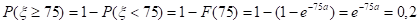
Откуда находим параметр...
