Условие задачи
Раскройте тему:
Выборочная дисперсия и исправленная дисперсия.
Ответ
Для того, чтобы наблюдать рассеяние количественного признака значений выборки вокруг своего среднего значения, вводят сводную характеристику- выборочную дисперсию.
Выборочной дисперсией называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения.
Если все значения признака выборки различны, то
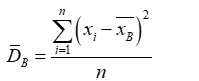
если же все значения имеют частоты n1, n2,, nk, то
Потяни
