Условие:
В таблице представлены наблюдения случайной величины Х. Для данных наблюдений:
1) Определите выборочное распределение случайной величины Х
2) Получите оценки математического ожидания и дисперсии случайной величины Х.
3) Определите для них 95% доверительные интервалы;
4) Считая, что случайная величина Х подчиняется биномиальному распределению (число опытов определяется наибольшим значением Х) рассчитайте ее теоретическое распределение;
5) По критерию Пирсона с уровнем значимости 0,05 проверьте гипотезу о биномиальном распределении случайной величины Х.

Решение:
1) Составим таблицу частот случайной величины Х. Для этого определим диапазон ее значений. Наименьшее значение Х равно 2, наибольшее значение равно 5.
Подсчитаем количество наблюдений.
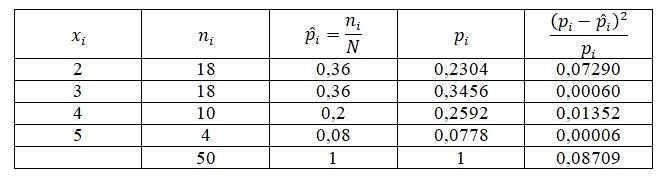
Рассчитаем частости (относительные частоты) случайной величины Х. Для этого разделим частоты на число наблюдений N. Получим выборочное распределение, которое представлено в третьей строке таблицы.
2) Оценка математичес...
