Условие:
По заданным уравнениям движения точки М в декартовых координатах x = f1(t), y = f2(t) найти:
1) уравнение траектории движения точки;
2) скорость и ускорение точки в произвольный момент времени t, а также в момент времени t = t1;
3) касательное и нормальное ускорения точки в момент времени t1;
4) радиус кривизны траектории в момент времени t = t1.
Кроме того, построить, выбрав соответствующие масштабы для длин, скоростей и ускорений:
1) траекторию точки;
2) положение точки на траектории в момент временя t = t1;
3) скорость и ускорение точки, а также касательное и нормальное ускорения для момента времени t = t1.
Дано:
x = 3sin(π t/6) см, y = 2 + 4cos(π t/6) см, t1 = 1 с.
Решение:
1. Исследование траектории.
Получим уравнение траектории точки в форме зависимости 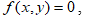 исключив параметр t из уравнений движения.
исключив параметр t из уравнений движения.
Имеем:
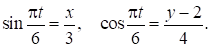
Используя основное тригонометрическое тождество, получаем уравнение...
