Условие:
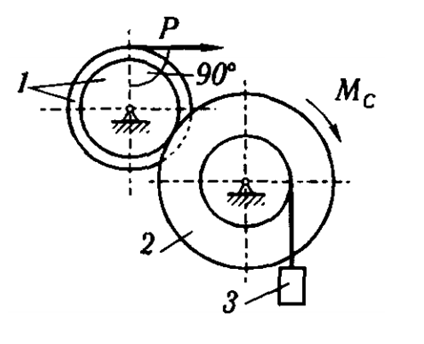
Механическая система состоит из механизма (колёс 1 и 2) и груза 3.
К колесу 1 приложена пара сил с моментом M=M(t) (движущий момент) или движущая сила P=P(t).
Время t отсчитывается от некоторого момента (t=0), когда φ0=0, а угловая скорость колеса 1 равна ω10. Момент сил сопротивления ведомого колеса 2 равен МС. Другие силы сопротивления движению системы не учитывать.
Массы колёс 1 и 2 равны m1 и m2, а масса груза 3 – m3.
Радиусы больших и малых окружных колёс R1, r1, R2, r2.
Найти уравнение движения тела системы. Определить натяжение нитей в заданный момент времени, найти окружное усилие в точке касания колёс 1 и 2.
Дано:
m1 = 150 кг; m2 = 300 кг; m3 = 700 кг;
R1 = 40 см; r1 = 30 см; R2 = 60 см; r2 = 30 см;
ix1 = 30 см; ix2 = 40 см;
P = 3900+50t;
МС = 1000 Нм;
ω10 = 1 рад/с;
t1 = 2 c;
Найти:
уравнение φ1 = f(t) вращательного движения колеса 1 механизма,
окружное усилие S в точке касания колёс 1 и 2,
натяжения нити в момент времени t1 = 2 c.
Решение:
В данной механической системе колёса 1 и 2 механизма вращаются вокруг неподвижных осей, а поднимаемый груз 3 совершает поступательное движение.
Напишем дифференциальные уравнения движения каждого из этих трёх тел, для чего отделим одно от другого, разрезав нить, удерживающую груз 3, и разделив колёса 1 и 2 в точках соприкасания.
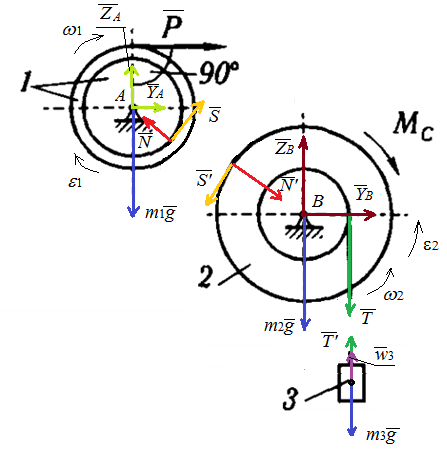
К колесу 1 механизма приложена сила тяжести сила составляющие реакции...
