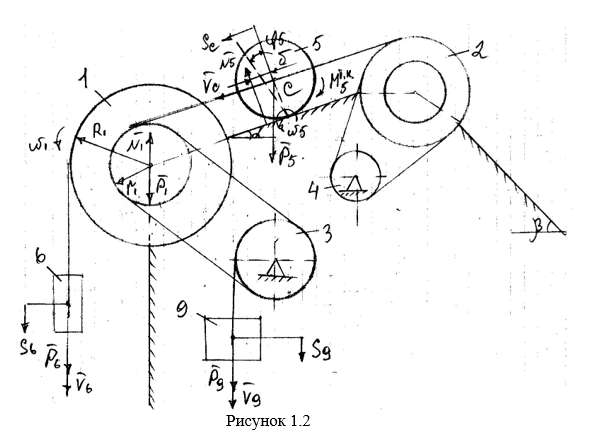
Механическая система состоит из ступенчатых шкивов, колес, блоков и грузов. Для тел 1, 2, 3 заданы радиусы инерции относительно оси вращения, масса тела 4 равномерно распределена по внешнему ободу, тело 5 считать однородным цилиндром.
- Теоретическая механика
Условие:
Механическая система состоит из ступенчатых шкивов, колес, блоков и грузов. Для тел 1, 2, 3 заданы радиусы инерции относительно оси вращения, масса тела 4 равномерно распределена по внешнему ободу, тело 5 считать однородным цилиндром. Тела системы соединены друг с другом гибкими невесомыми нерастяжимыми нитями, которые или перекинуты через блоки или намотаны на шкивы, участки нитей параллельны соответствующим плоскостям. Некоторые тела соединены ременными или фрикционными передачами. Радиусы тел и радиусы инерции указаны. Массы тел приведены. Прочерк в таблице означает, что тело отсутствует и изображать его не надо. Если масса тела равна нулю, то данное тело показывается на рисунке, но его массой при расчетах следует пренебречь. В некоторый момент времени под действием сил тяжести система приходит в движение из состояния покоя. При скольжении по плоскостям на грузы действуют силы трения, коэффициент трения скольжения f. Качение всех тел происходит без скольжения, при этом для случая качения тел по неподвижным плоскостям следует учитывать трение качения, коэффициент трения качения δ. Трением в осях вращения пренебречь. Длины нитей и длины участков достаточны для того, чтобы тела при движении не сталкивались друг с другом. Определить скорость груза, указанную в столбце «Найти», после того как этот груз переместится на расстояние S. При этом нужно указать, в какую сторону этот груз движется.
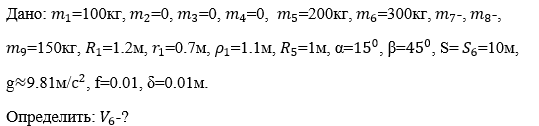
Решение:
Для определения скорости груза 6 применим теорему об изменениикинетической энергии системы в интегральной форме:
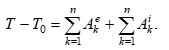
Для рассматриваемой системы, состоящей из абсолютно твёрдых тел,соединённых нерастяжимыми нитями, начинающей движение из состоянияпокоя, начальная кинетическая энергия и сумма работ внутренних сил будутравны:
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства