Условие задачи
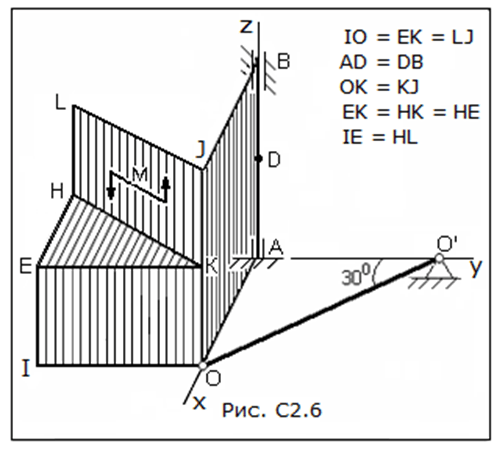
Несколько тонких однородных пластин различной геометрической формы приварены друг к другу и образуют некоторую пространственную фигуру, движение которой ограничено связями в точках А, В, О. Размеры пластин параллельных координатным плоскостям в направлениях осей х, у, z, равны соответственно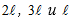 
(рис. С2.0 – С2.4), или 
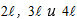(рис. С2.5 – С2.9). Удельный вес площади горизонтальных и вертикальных пластин γ1 = 1 кН/м2, пластин наклоненных к горизонту γ2 = 2 кН/м2 .
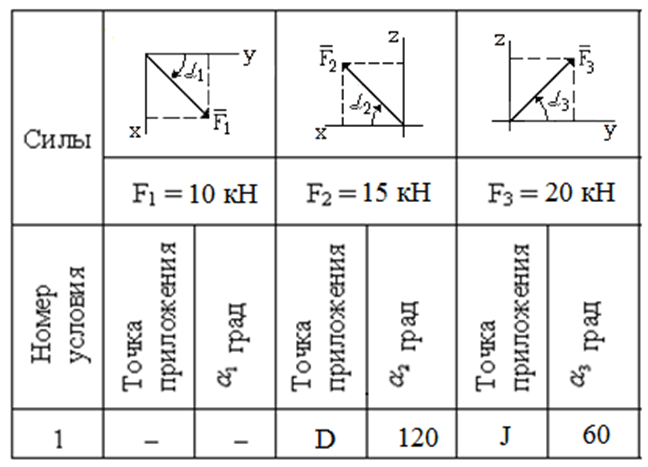
Кроме сил тяжести на пластины действуют пара сил с моментом М = 10 кН×м, лежащая в плоскости одной из пластин, и две силы. Величины этих сил, их направления и точки приложения указаны в табл. С2; при этом силы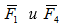 
лежат в плоскостях, параллельных плоскости хАу, сила 
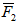− в плоскости параллельной хАz, и сила 
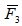в плоскости, параллельной уАz. Определить:
− величину силы тяжести конструкции и координаты ее центра тяжести (учитывать только пластины, у которых на рисунке видна хотя бы часть поверхности),
− реакции связей конструкции.
При расчетах принять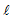 
= 0,5 м. Толщиной пластин пренебречь.
Ответ
1. Определение координат центра тяжести конструкции
Изобразим рассматриваемую конструкцию, не показывая действующих на нее сил.
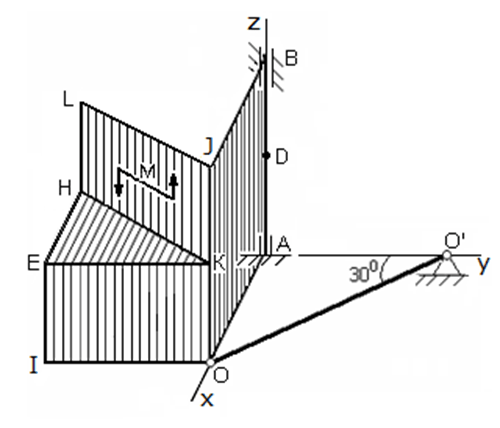
Рис. 1
Для решения задачи применим метод разбиения тела на части.
Разобьем рассматриваемую конструкцию на четыре части (пластины): пластину ABJO ей присвоим номер 1, пластину LHKJ номер 2, пластину KEIO номер 3, пластину KEH номер 4.
