Условие задачи
Механическая система состоит из нескольких тел, соединенных между собой с помощью тросов, как показано на рис.1. Под действием сил тяжести она приходит в движение из положения покоя, при этом преодолеваются силы трения скольжения и качения по наклонной плоскости, определяемые коэффициентами f и δ. Кроме этого, движению препятствует момент сопротивления Mc на ступенчатом блоке 2, обусловленный трением в подшипниках. Плоскости наклонены к горизонту под углами α и β, а масса тел составляет m1=200кг, m2=30кг. Радиусы колес и блоков соответственно равны R2=20см, r2=10см, R3=15см. Радиус инерции ρ2=16см, а масса тела 3 равномерно распределена по его ободу. Угол наклона плоскости β=30°.
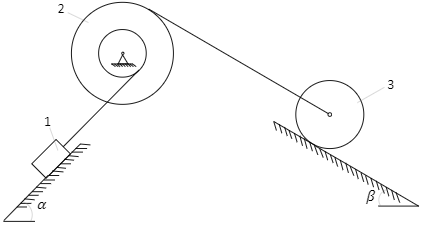
Рисунок 1.
Пренебрегая массой соединительных тросов, определить величину и направление скорости тела 1 и угловой скорости блока 2 в момент времени, когда он повернется на угол φ2=1,5π. Считать, что момент сопротивления Mc направлен против движения независимо от того, в какую сторону будет перемещаться система, а качение катков (блоков) 3 происходит без проскальзывания.
Ответ
Дано: Mc=5Н∙м; m3=140кг; =90; =0,02м.
Используем заданную по варианту исходную схему и предположим, что под действием сил груз 1 движется вертикально вниз. Тогда скорости точек и тел системы будут соответствовать представленным на рис. 2.
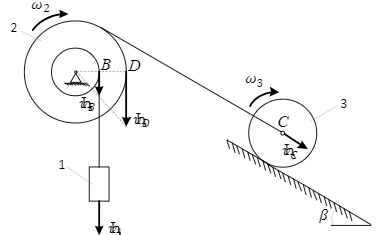
Рисунок 2.
Учитывая, что тросы принято считать нерастяжимыми, перемещения тел определяются углом поворота 2, а время действия сил не задано, то для решения задачи у...
