Условие:
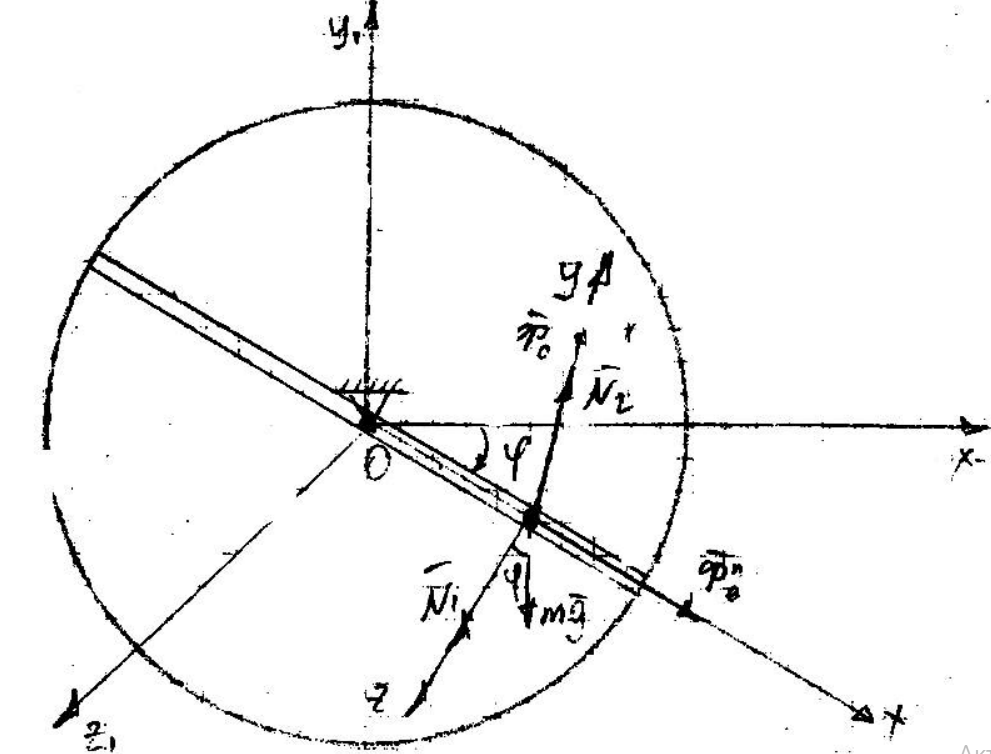
Шарик M, рассматриваемый как материальная точка массы m перемещается внутри гладкого канала диска. При этом диск вращается вокруг неподвижной горизонтальной оси Oz1, перпендикулярной диску, с постоянной угловой скоростью 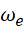 .
.
Найдите уравнение относительного движения точки x=x(t), значение координаты x=x(t), а также давление точки на стенку канала N в момент времени t=t1 .
Дано:
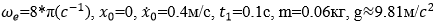
Определить:
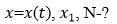
Решение:
Будем считать движение материальной точки М по диску относительнымдвижением, а вращение диска- переносным движением. Составимдифференциальное уравнение относительного движения точки М:
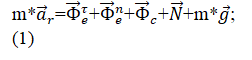
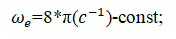
Интегрируем:
