Условие:
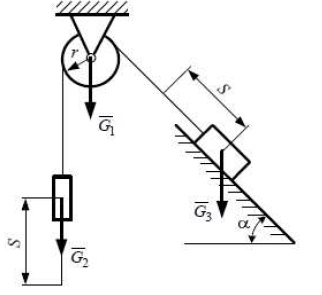
Через однородный блок весом G1 и радиусом r перекинут трос с двумя грузами G2 и G3. Груз G2 опускается (или поднимается) по вертикали, груз G3 поднимается (или опускается) по гладкой наклонной плоскости с углом наклона α. Массой троса и сопротивлениями в опорах - пренебречь.
Исходыне данные: G1 = 24 кН, G2 = 40 кН, G3 = 200 кН, v = 3,5 м/с, r = 0,3 м, α = 45º.
Груз G2 - движется вверх.
Требуется определить: 1) высоту S, на которую должен опуститься (или подняться) груз G2, чтобы достичь скорости v, если начальная скорость равна нулю;
2) ускорение a движения грузов.
Решение:
1. Скорость движения грузова равна по величине скорости на окружности блока. Следовательно, угловую скорость блока можно определить по формуле:
𝜔 = v/r.
Запишем закон сохранения кинетической энергии для рассматриваемой механической системы:
К2 - К1 = АFi. (1), так как начальная скорость по условию задачи р...
