Рассмотрим антагонистическую игру двух лиц с нулевой суммой – модель конфликтной ситуации с двумя участниками, в которой выигрыш одного равен проигрышу другого. Пусть игрок А располагает m чистыми стратегиями, т.е. возможными действиями
- Теория игр
Условие:
Рассмотрим антагонистическую игру двух лиц с нулевой суммой – модель конфликтной ситуации с двумя участниками, в которой выигрыш одного равен проигрышу другого. Пусть игрок А располагает m чистыми стратегиями, т.е. возможными действиями: A1, A2, ..., Am, а игрок В – n чистыми стратегиями: B1, B2, ..., Bn. Чтобы игра была полностью определенной, необходимо указать правило, сопоставляющее каждой паре чистых стратегий Ai и Bj число aij - выигрыш игрока А за счет игрока В или проигрыш игрока В. При aij <0 игрок А платит игроку В сумму |aij| . Если известны значения aij для каждой пары (Ai , Bj) чистых стратегий, то можно составить матрицу игры – платежную матрицу.
Для игр, заданных следующими платежным матрицами, найти нижнюю и верхнюю чистые цены, максиминную и минимаксную стратегии игроков, установить наличие седловых элементов в платежных матрицах (в последнем случае найти решение игры):
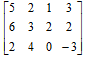
Решение:

Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства