Условие задачи
4 пассажиров садятся в электричку, состоящую из 8 вагонов. Каждый пассажир выбирает свой вагон случайным образом независимо от других, так что с одинаковой вероятностью может оказаться в любом из вагонов. Рассматриваются события:
A = {первый пришедший пассажир садится в первый вагон, последний – в последний};
B = {все пассажиры окажутся в первых 4 вагонах};
C = {все пассажиры сядут в разные вагоны}.
1. Выбрать соответствующее множество в качестве пространства элементарных исходов рассматриваемого испытания и с помощью его элементов описать события А, В, С.
2. Проверить попарную несовместимость событий А, В, С.
3. Проверить образуют ли события А, В, C полную группу событий.
4. Используя классическое или геометрическое определение вероятности, найти вероятности событий А, В, С.
5. Используя теоремы сложения и умножения найти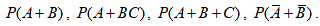 
6. Проверить парную и взаимную независимость событий А, В, С.
Ответ
1. Всего существует 84 = 4096 способов рассадить пассажиров по вагонам:
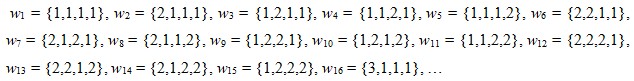
То есть элементарный исход имеет вид , где номер элементарного исхода, номер выбранного вагона первым, вторым, третьим и четвертым пассажиром соответственно.
