Условие задачи
Дана плотность нормально распределенной случайной величины:
Найти математическое ожидание, стандартное отклонение, дисперсию и вероятность того, что в результате испытания случайная величина примет значение в интервале (3;4).
Ответ
Плотность распределения вероятностей для нормального распределения имеет вид:
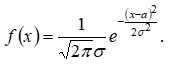
Здесь а математическое ожидание, - среднее квадратическое отклонение, тогда из формулы плотности получим:
Потяни
