Пусть X_1, X_2, ... X_n – выборка из заданного в соответствии с вариантом закона распределения. Неизвестные параметры: 𝒂 Известные параметры: 𝝀 = 𝟏, 𝜶 = 𝟒
- Теория вероятностей
Условие:
Пусть X1, X2, ... Xn – выборка из заданного в соответствии с вариантом закона распределения.
Неизвестные параметры: 𝒂
Известные параметры: 𝝀 = 𝟏, 𝜶 = 𝟒
Двустороннее экспоненциальное распределение:
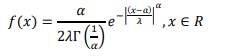
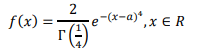
1. Найти числовые характеристики заданной модели:
a. математическое ожидание
b. дисперсию
2. Найти точечную оценку неизвестного параметра Θ
a. по методу моментов
b. по методу максимального правдоподобия
3. Проверить условия регулярности модели. В случае регулярности модели, вычислить информационное количество Фишера 𝒊(𝜽)
4. Подобрать удобную параметрическую функцию τ для исследования свойств оценок. Записать оценку 𝝉̂(𝜽) на основании любой оценки 𝜽 из п.1. Проверить свойства 𝝉̂(𝜽):
a. несмещенность
b. состоятельность
c. эффективность (не используя критерий эффективности)
5. Найти достаточную статистику для заданной модели
6. Найти функцию 𝝉(𝜽), допускающую эффективную оценку (с помощью критерия эффективности)
7. Построить асимптотический доверительный интервал для Θ
Решение:
1. Найти числовые характеристики заданной модели:
a. математическое ожидание
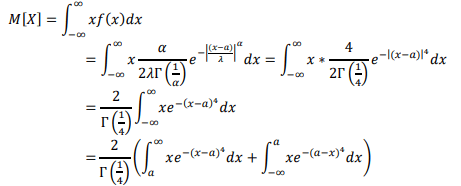
Решим интеграл
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства