Экзаменатор задает студенту дополнительные вопросы, но не более . Вероятность того, что студент ответит на любой заданный вопрос, равна Экзаменатор прекращает опрос, как только студент обнаруживает незнание заданного вопроса.
- Теория вероятностей
Условие:
Экзаменатор задает студенту дополнительные вопросы, но не более n = 5. Вероятность того, что студент ответит на любой заданный вопрос, равна p = 0,98. Экзаменатор прекращает опрос, как только студент обнаруживает незнание заданного вопроса.
Требуется:
1) составить закон распределения ДСВ X – числа дополнительных вопросов, которые задает преподаватель;
2) представить закон распределения графически;
3) составить функцию распределения F(X) и построить ее график;
4) вычислить начальные и центральные моменты СВ X до 4-го порядка включительно, коэффициент асимметрии и эксцесса;
5) указать числовые характеристики, которые описывают положение центра распределения и рассеивания СВ относительно ее среднего значения;
6) объяснить, какое распределение вероятностей называется биномиальным, Пуассона и геометрическим. Чему равны числовые характеристики этих распределений.
Решение:
1) Т.к. вероятность того, что студент ответит на заданный вопрос, равна p =0,98, то вероятность не ответить на вопрос равна 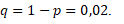
ДСВ X числа дополнительных вопросов, которые задает преподаватель может принимать значения от 1 до 5. Вычислим соответствующие вероятности:
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства