Условие задачи
1. Ответьте на вопросы: Эргодичен ли этот марковский процесс? Почему? (приведен граф состояний).
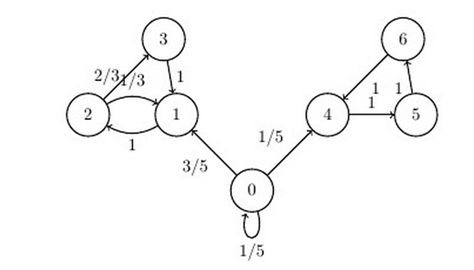
2.
На острове Безмятежности бывает три типа погоды: солнечно, дождливо и сухо, но облачно. Солнечный день сменяется дождливым с вероятностью 0,2 и с вероятностью 0,2 сменяется облачным сухим. Каждый дождливый день сменяется солнечным с вероятностью 0,4, с вероятностью 0,4 облачным сухим. Каждый облачный сухой день сменяется солнечным с вероятностью 0,4 и с вероятностью 0,2 дождливым.
а) Сегодня солнечно на о. Безмятежности. Каков шанс дождя послезавтра?
б) Спрогнозировать сколько следует ожидать дождливых дней ежегодно.
Ответ
1.
Поскольку в эргодичных марковских процессах возможен переход из любого состояния в любое другое за конечное число шагов, приведенный граф соответствует неэргодичному марковскому процессу, т.к. для множества вершин и возможны переходы только между вершинами соответсвующих множеств.
2.
Рассмотрим последовательность смены погоды как дискретную цепь Маркова с тремя состояниями, соответствующими типам погоды: S1 солнечно, S2 дождливо, S3 сухо, но облачно. Согласно приведенному условию, получаем матрицу переходом между состояниями за один шаг (недостающие вероятности сохранения погодына следующий ...
