Условие задачи
Игральный кубик бросают 2 раза. Написать закон распределения случайной величины – числа выпадений грани с пятью очками. Вычислить математическое ожидание и среднеквадратическое отклонение.
Ответ
Найдем закон распределения СВ Х числа выпадений грани с пятью очками.
СВ Х может принимать значения 0,1,2.
Вероятность выпадения грани с пятью очками при каждом броске равна 1/6 и не зависит от других бросков, следовательно, вероятности значений СВ Х найдем по формуле Бернулли: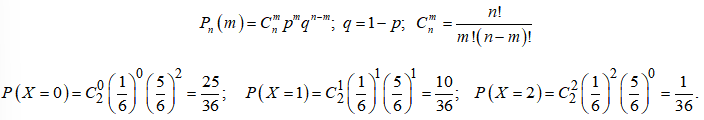
Закон (ряд) распределения случайной величины Х:
Потяни
