Условие:
Из 100 конденсаторов за время Т из строя выходят 5 конденсаторов. Для контроля выбирают 8 конденсаторов. Используя классическое определение вероятности, формулу Бернулли, формулу Пуассона и локальную теорему Лапласа, найти вероятность того, что среди них за время Т из строя выйдет ровно 1 конденсатор.
Решение:
Найдем вероятность того, что из 8 выбранных конденсаторов за время Т из строя выйдет ровно 1 конденсатор, используя классическое определение вероятности. Общее число исходов равно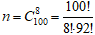 
. Число благоприятных исходов равно . Тогда по классическому определению вероятности искомая вероятность равна: