Условие задачи
Из двух независимых генеральных совокупностей, распределённых по нормальному закону с неизвестными, но равными (𝐷(𝑋) = 𝐷(𝑌)) дисперсиями, извлечены выборки объёмов 𝑛 = 8 и 𝑚 = 10 соответственно, для которых вычислены выборочные средние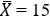 
и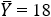 
и выборочные дисперсии 𝐷в(𝑋) = 2 и 𝐷в(𝑌)= 3. На уровне значимости 𝛼 = 0,02 проверить гипотезу о равенстве математических ожиданий генеральных.
Ответ
Обозначим нулевую гипотезу Н0: М(Х) = М(Y) равенство математических ожиданий (генеральных средних) двух нормальных совокупностей, дисперсии которых неизвестны. Конкурирующая гипотеза Н1: М(Х) М(Y).
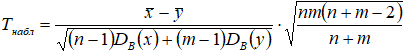
который распределен по закону Стьюдента с степенями свободы.
Потяни
