1. Главная
  2. Библиотека
  3. Теория вероятностей
  4. На столе лежит стопка из четырех книг. Каждая книга берется для чтения с вероятностью ¼, а при возвращении она с вероятнос...

На столе лежит стопка из четырех книг. Каждая книга берется для чтения с вероятностью ¼, а при возвращении она с вероятностью 2/3 кладется сверху, либо с вероятностью 1/3 на ... На столе лежит стопка из четырех книг. Каждая книга берется для чтения

«На столе лежит стопка из четырех книг. Каждая книга берется для чтения с вероятностью ¼, а при возвращении она с вероятностью 2/3 кладется сверху, либо с вероятностью 1/3 на ... На столе лежит стопка из четырех книг. Каждая книга берется для чтения»
  • Теория вероятностей

Условие:

На столе лежит стопка из четырех книг. Каждая книга берется для чтения с вероятностью ¼, а при возвращении она с вероятностью 2/3 кладется сверху, либо с вероятностью 1/3 на прежнее место.

С какой вероятностью i-я (i=1,2,3,4) книга окажется наверху через достаточно большое время? (Применение эргодической теоремы обосновать)

Решение:

Представим последовательность перемещения книг марковской цепью с четырьмя состояниями 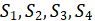верхней книгой в стопке лежит 1, 2, 3 и 4 книга соответственно.

Определим вероятности переходов между состояниями:

- пусть верхней книгой в стопке лежит первая книга.

Тогда с вероятностью следующей книгой, лежащей сверху, может оказаться любая из книг 2-4, а с вероятностью верхней останется первая книга;

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я