![Найти в антагонистической игре седловую точку, если она есть. X = [0; 1]; Y = [0; 1]; F(x, y) = sin(π / 2 • x • y). Так как нижняя цена игры совпадает с верхней ценой игры, то игра имеет седловую точку (0; 0). Цена игры v = 0.](/public/images/library/external/library-detail-hero-book.png)
Условие:
Найти в антагонистической игре седловую точку, если она есть. X = [0; 1]; Y = [0; 1]; F(x, y) = sin(π / 2 · x · y).
Решение:
Находим вторую частную производную по x от функции выигрыша F(x, y) = sin( / 2 x y): 2F/x2 = ( / 2 y)2 sin( / 2 x y). Очевидно, что при x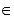 
(0; 1) и y 
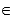(0; 1) имеем
2F/x2 0. Это значит, что F(...