Найти вероятности следующих событий: A – встреча состоялась; B – Ивану не пришлось ждать Петра; C – Петр опоздал на встречу.
«Найти вероятности следующих событий: A – встреча состоялась; B – Ивану не пришлось ждать Петра; C – Петр опоздал на встречу.»
- Теория вероятностей
Условие:
Иван и Петр договорились о встрече в определенном месте между T1 и T2 часами. Каждый приходит в случайный момент указанного промежутка и ждет появления другого до истечения часа, но не более t1 минут, после чего уходит. Наблюдаемый результат – пара чисел (x,y), где x – время прихода Петра, y – время прихода Ивана (время исчисляется в минутах, начиная с T1 часов). Найти вероятности следующих событий: A – встреча состоялась; B – Ивану не пришлось ждать Петра; C – Петр опоздал на встречу.
Решение:
T1 = 12-00, T2 = 12-30, t1 = 6.
Будем считать интервал от 12-00 до 12-30 отрезком длиною 1/2.
По условию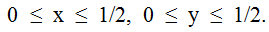 
Этим неравенствам удовлетворяют координаты любой точки, принадлежащей квадрату OKLM со стороной, равной 1/2.
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э