«Определение вероятности прихода в конечную точку на основе метода Монте-Карло (задача о случайном блуждании)» Человек решает прогуляться, находясь на углу улицы. Пусть вероятность того, что он пойдет на север равна Х, на юг равна А,
- Теория вероятностей
Условие:
Выполнить лабораторную работу:
«Определение вероятности прихода в конечную точку на основе метода Монте-Карло (задача о случайном блуждании)»
Человек решает прогуляться, находясь на углу улицы. Пусть вероятность того, что он пойдет на север равна Х, на юг равна А, на восток - В и на запад равна С. Какова вероятность того, что пройдя М кварталов человек окажется не дальше К кварталов от того места, где он начал прогулку.
1. Разработка Генератора случайных чисел (ГСЧ), имеющих равномерное распределение на интервале [0,1] (Использование стандартной функции).
2. Получение N случайных чисел и их использование для расчета направления движения в городе на основе метода Монте-Карло.
3. Расчет вероятности прихода в нужную точку (Р=Nп/N, где Nп – количество приходов в нужную точку, N - общее количество испытаний).
Выводы о возможности использования метода Монте-Карло для расчета вероятности прихода в нужную точку.
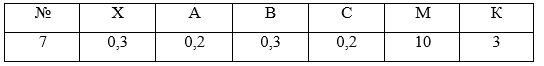
Решение:
Для моделирования направления движения воспользуемся базовым равномерным распределением R(0;1) и следующими правилами:
- если значение R0,3, то считаем, что человек на углу улицы пойдет на север;
- если значение 0,3R0,5, то считаем, что человек на углу улицы пойдет на юг;
- если значение 0,5R0,8, то считаем, что человек на углу улицы пойдет на восток;
- если значение R0,8, то считаем, что человек на углу улицы пойдет на запад.
Далее, для определения расстояния от исходной точки будем...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства