Условие задачи
Провести идентификацию эмпирической математической модели в случаях А) и Б).
А) Предполагается, что процесс описывается одномерным уравнением 2-го порядка W=a0+a1x+a2x2, 0≤x≤10.
Б) Предполагается, что процесс описывается одномерным уравнением 3-го порядка W=a0+a1x+a2x2+a3x3, 0≤x≤10.
Считаем, что величина х измеряется точно, а W – с ошибкой ε, имеющей нормальное распределение с нулевым математическим ожиданием и единичной дисперсией М(ε)=0, 𝜎2(ε)=1. Проверить адекватность модели методом Фишера и сравнить модели А) и Б) графически с моделью линейной регрессии.
Ответ
Под идентификацией эмпирической математической модели понимается оценка параметров модели (коэффициентов).
Для нахождения коэффициентов уравнения применим метод наименьших квадратов (МНК). Для этого необходимо минимизировать функцию:
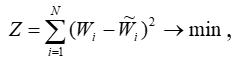
где N число наблюдений в выборке, отклонения (остатки).
