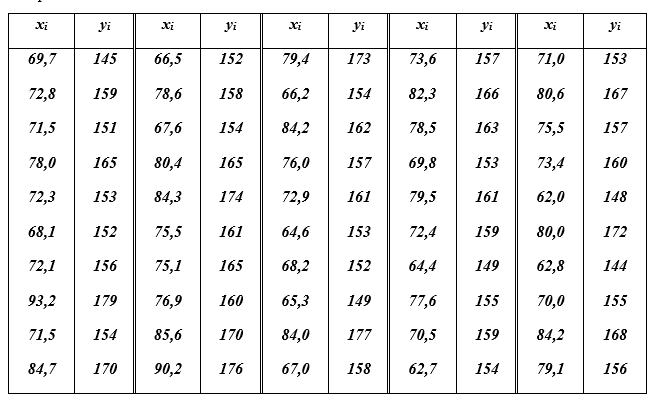
Пусть двумерная случайная величина (X, Y) – генеральная совокупность, где Х – вес (в килограммах), а Y – рост (в см) случайно взятого человека. В качестве исходных данных студенту предлагается выборка объёмом 50 из генеральной совокупности (X, Y).

Пусть двумерная случайная величина (X, Y) – генеральная совокупность, где Х – вес (в килограммах), а Y – рост (в сантиметрах) случайно взятого человека. В качестве исходных данных студенту предлагается выборка 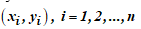объёмом n = 50 из генеральной совокупности (X, Y). 
Для статистической обработки этих данных в контрольной работе требуется выполнить следующее задание:

1. Для величин Х и Y составить группированные ряды. Построить полигоны, гистограммы относительных частот.
2. Вычислить точечные оценки: выборочные средние   и  ; несмещённые выборочные средние квадратичные отклонения sx и sy.
3. Проверить гипотезы о нормальном законе распределения случайных величин Х и Y при уровне значимости a = 0,05.
4. Найти доверительные интервалы для M(X), M(Y), D(X), D(Y) с доверительной вероятностью g = 0,95.
5. Составить корреляционную таблицу. Вычислить выборочный коэффициент корреляции rв.
6. Найти выборочные уравнения прямых линий регрессии Y на Х и Х на Y. Построить графики этих прямых на одном рисунке с наблюдаемыми точками (xi, yi),  i = 1, ..., n.