Условие задачи
Система S может находиться в 4-х состояниях. В системе протекает марковский процесс с дискретным временем. Размеченный граф состояний этой системы:
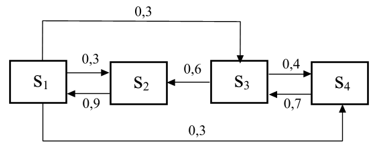
В начальный момент времени система находится во 2-м состоянии.
Найти вероятности состояний на 3-м шаге. Проверить, является ли марковская цепь регулярной. Найти предельные вероятности состояний, если они существуют.
Ответ
Запишем матрицу переходных вероятностей за один шаг (значения диагональных элементов находим из условия нормировки j pi,j =1):

Последовательно найдем матрицу переходных вероятностей за два и три шага соответственно:









