Главная
Библиотека
Теория вероятностей
Случайная величина X распределена нормально с математическим ожиданием M(X)=25. Вероятность попадания X в интервал (10;15)...

Случайная величина X распределена нормально с математическим ожиданием M(X)=25. Вероятность попадания X в интервал (10;15) равна 0,2. Найти вероятность попадания X в интервал (35;40).

«Случайная величина X распределена нормально с математическим ожиданием M(X)=25. Вероятность попадания X в интервал (10;15) равна 0,2. Найти вероятность попадания X в интервал (35;40).»

8 августа 2024
Теория вероятностей

Условие:

1. Случайная величина X распределена нормально с математическим ожиданием M(X)=25. Вероятность попадания X в интервал (10;15) равна 0,2. Найти вероятность попадания X в интервал (35;40).

2. Случайная величина X распределена по нормальному закону с параметрами a=6, Найти вероятность того, что случайная величина X окажется в интервале (3;7).

3. Случайная величина X задана функцией распределения:

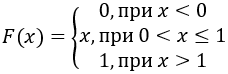
Найти вероятность того, что в результате четырех испытаний случайная величина X ровно 3 раза примет значение из интервала (0,3;0,7).

4. Автомат штампует детали. Контролируется длина детали X, которая является случайной величиной, распределенной по нормальному закону с математическим ожиданием (проектная длина) равным 50 мм. Фактически длина изготовленных деталей не менее 32 мм и не более 62 мм. Найти вероятность того, что длина наудачу взятой детали: а) более 55 мм; б) менее 40 мм.

Решение:

1. Так как нормальная кривая симметрична относительно прямой x=a=25, то площади, ограниченные сверху нормальной кривой и снизу интервалами (10;15) и (35;40), равны между собой. Поскольку эти площади численно равны вероятностям попадания X в соответствующий интервал, то:

P(10X15)=P(35X40)=0,2

Ответ: 0,2