1. Главная
  2. Библиотека
  3. Теория вероятностей
  4. В фирменный магазин поступает пуассоновский поток с интенсивностью λ=200 покупателей в час. В течение дня их обслуживает n...

В фирменный магазин поступает пуассоновский поток с интенсивностью λ=200 покупателей в час. В течение дня их обслуживает n=3 контролеров-кассиров с интенсивностью μ=90 покупателей в час. Интенсивность выходного потока покупателей в часы пик

«В фирменный магазин поступает пуассоновский поток с интенсивностью λ=200 покупателей в час. В течение дня их обслуживает n=3 контролеров-кассиров с интенсивностью μ=90 покупателей в час. Интенсивность выходного потока покупателей в часы пик»
  • Теория вероятностей

Условие:

В фирменный магазин поступает пуассоновский поток с интенсивностью λ=200 покупателей в час. В течение дня их обслуживает n=3 контролеров-кассиров с интенсивностью μ=90 покупателей в час. Интенсивность выходного потока покупателей в часы пик возрастает до λmax=400, а в часы спада достигает величины λmin=100.

Определите вероятность образования очереди в магазине Pоч и среднюю длину очереди 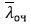в течение дня, а затем необходимое число контролеров в часы пик n_max и часы спада n_min, обслуживающих такую же длину очереди 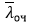, и вероятность её образования Pоч.

Решение:

В этой задаче возникает многоканальная СМО с ожиданием.

Запишем условие задачи:

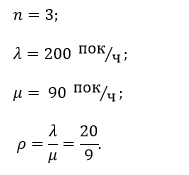
Условие устойчивой работы СМО n=20271 выполнено.

Вероятность покупателя оказаться в очереди имеет вид

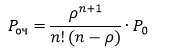
Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я