В первой урне m один = шесть белых и n один = шесть черных шаров, во второй – m два = семь белых и n два = шесть черных. Из второй урны случайным образом перекладывают в первую два шара, после чего из первой урны берут один шар.

Рассмотрим зависимое событие (после перемещения двух шаров из первой урны будет извлечен белый шар) и предшествующие ему несовместные события: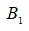
- из второй урны в первую будут переложены два белых шара;
- из второй урны в первую будут переложены один белый шар и один черный;