Условие задачи
В урне 3 белых и 2 черных шаров. Из нее три раза подряд извлекают шар, причем первый вынутый шар возвращают в урну, а остальные – нет.
Случайные величины: 𝑋 – число извлеченных белых шаров; 𝑌 – число черных шаров.
Для заданных случайных величин X и Y:
1) построить таблицу совместного распределения;
2) найти частные распределения для X и Y и вычислить для каждого из них математическое ожидание и дисперсию;
3) найти коэффициент корреляции;
4) определить, зависимы или независимы случайные величины X и Y.
Ответ
1) построить таблицу совместного распределения
Случайная величина X число извлеченных белых шаров имеет следующие возможные значения 0, 1, 2, 3. Случайная величина Y число черных шаров - имеет следующие возможные значения 0, 1, 2, 3.
Найдем вероятности
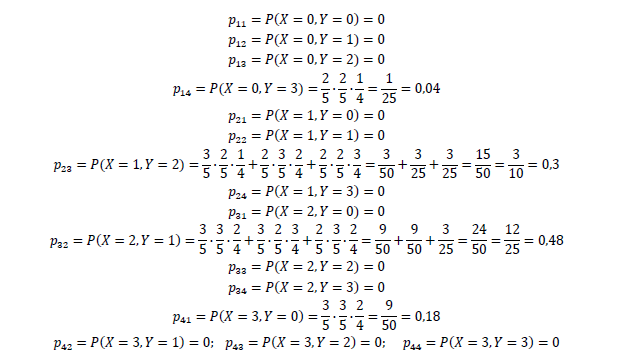
Таблица совместного распределения имеет вид
