1. Главная
  2. Библиотека
  3. Теория вероятностей
  4. Задан закон распределения двумерной дискретной случайной величины (X, Y): Требуется найти: a) неизвестную вероятность р; b...

Задан закон распределения двумерной дискретной случайной величины (X, Y): Требуется найти: a) неизвестную вероятность р; b) законы распределения компонент X и Y, функции распределения компонент; c) числовые характеристики одномерных случайных величин X и

«Задан закон распределения двумерной дискретной случайной величины (X, Y): Требуется найти: a) неизвестную вероятность р; b) законы распределения компонент X и Y, функции распределения компонент; c) числовые характеристики одномерных случайных величин X и»
  • Теория вероятностей

Условие:

Задан закон распределения двумерной дискретной случайной величины (X, Y):

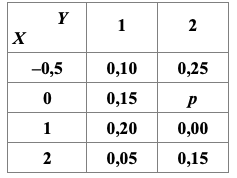
Требуется найти:

a)  неизвестную вероятность р;

b)  законы распределения компонент X и Y, функции распределения компонент;

c)  числовые характеристики одномерных случайных величин X и Y и числовые характеристики двумерной случайной величины (X,Y);

d)  корреляционный момент КXY и коэффициент корреляции rXY.

Решение:

а) Так как двумерная случайная величина принимает только приведенные значения, то сумма их вероятностей равна 1. Отсюда находим неизвестную вероятность р:

р = 1 (0,10+0,25+0,15+0,20+0,05+0,15) = 0,10

Тогда закон распределения двумерной дискретной случайной величины (X, Y) имеет вид:

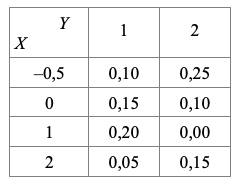
b) Закон распределения компонента X определяем, суммируя вероятности по строкам:

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я