Стальной слиток, имеющий форму параллелепипеда с размерами имел начальную температуру t0, С, а затем был помещен в печь с температурой tж, С.

22 января 2025
Теплоэнергетика и теплотехника

Условие:

Стальной слиток, имеющий форму параллелепипеда с размерами 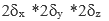имел начальную температуру t₀, °С, а затем был помещен в печь с температурой t_ж, °С.

Определить температуру t_н, °С в центре слитка, на поверхностях слитка и в средних точках соответствующих поверхностей по осям через время t, час, после загрузки его в печь.

Построить графики распределения температуры по сечениям болванки. Коэффициенты теплопроводности материала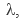Вт/(м С), температуропроводности материала, а, м²/с и значение коэффициента теплоотдачи на поверхности слитка a, Вт/(м² С).

Решение:

Дано:

Безразмерная температура любой точки параллелепипеда равна произведению безразмерных температур трех безграничных пластин, пересечением которых образован параллелепипед. Следовательно, температуру в центре параллелепипеда можно найти из уравнения