Условие:
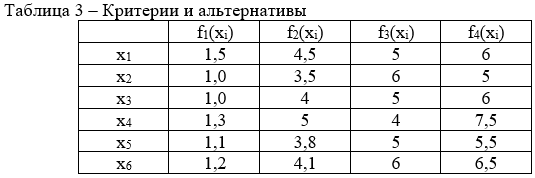
В ходе модернизации аэропорта рассматриваются проекты строительства нового терминала для приема пассажиров. Предлагаются 6 проектов, оценка которых производится по следующему набору критериев: (табл. 3):
f1 → max – пропускная способность, тыс. пассажиров в день;
f2 → min – затраты на строительство, млн. ден. ед.;
f3 → min – срок строительства, мес.;
f4 → min – стоимость обработки 1 пассажира, ден. ед.
Порядок важности критериев: f1 > f4 > f2 > f3.
1) на основе заданного порядка важности критериев установить числовые оценки их весов, используя метод простого ранжирования или пропорциональный метод;
2) привести оценки по всем критериям к единой безразмерной шкале путем нормировки критериев;
3) выбрать решение, используя следующие виды свёрток:
- аддитивная,
- мультипликативная,
- расстояние до идеала.
Убедиться, что во всех случаях получено Парето оптимальное решение.
Решение:
1. Аддитивная и мультипликативная сборная.
Для оценки степеней относительной важности (весов) критериев, воспользуемся пропорциональным методом, предположив, что ЛПР считает критерий f1 в важнее критерия f4 в 2 раза, критерий f4 важнее критерия f2 в 2 раза, критерий f2 в важнее критерия f3 в 2 раза (табл. 4).

1. Заменим критерий f2 на (-f2), критерий f3 на (-f3), критерий f4 на (-f4) и перейдем к ...
