1. показать, что на отрезке находится только один локальный минимум (или одно наименьшее значение); 2. найти локальный минимум или наименьшее значение данной функции на отрезке с точностью до методом золотого сечения;
- Высшая математика
Условие:
Дана функция
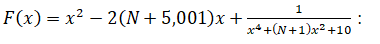
1. показать, что на отрезке 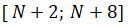 находится только один локальный минимум (или одно наименьшее значение);
находится только один локальный минимум (или одно наименьшее значение);
2. найти локальный минимум или наименьшее значение данной функции на отрезке 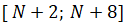 с точностью до
с точностью до 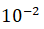 методом золотого сечения;
методом золотого сечения;
3. оценить интервал неопределенности локального минимума или наименьшего значения, принадлежащего отрезку 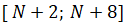 , если все расчеты проводятся с точностью до
, если все расчеты проводятся с точностью до 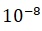 ;
;
4. оценить относительную погрешность найденного локального минимума или наименьшего значения по отношению к относительной погрешности коэффициента при x в первой степени 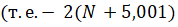 считая, что последняя равна 10%).
считая, что последняя равна 10%).
Решение:
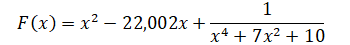
Покажем, что на отрезке [8;14] находится только один локальный минимум (или одно наименьшее значение).
Вычислим первую производную заданной функции:

Найдем ее значения на концах отрезка:
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства