Условие:
1. Решите уравнение 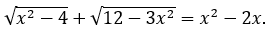
2. Какое наибольшее значение может принимать сумма косинусов всех углов равнобедренного треугольника?
Решение:
1. Прежде всего заметим, что все корни уравнения если они существуют, удовлетворяют неравенствам Так как второе неравенство равносильно неравенству то оба неравенства выполняются лишь при условии Это уравнение имеет два корня: x = 2 и x = -2. Итак, если исходное уравнение имеет корни, то их следует искать среди чисел 2 и -2. Проверка показывает, что 2 является корнем исходного уравнения, а число -2 нет. Следовательно, уравнение имеет единственный корень.
