Решение задачи
Дана функция двух переменныхДана функция двух переменных z= f ( x, y ). Требуется: а) составить уравнение линии уровня z=C и построить ее график;
- Высшая математика
Условие:
Дана функция двух переменных z= f ( x, y ). Требуется:
а) составить уравнение линии уровня z=C и построить ее график;
б) исследовать функцию z= f (x, y ) на экстремум;
в) вычислить градиент и производную f (x, y ) в точке A в направлении
вектора 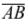 ;
;
г) найти наибольшую скорость изменения функции в точке A .
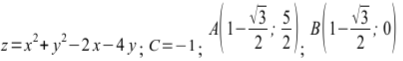 .
.
Решение:
а) Областью определения данной функции является множество точек (x, y )R2. Условие линий уровня z=C. Таким образом, необходимо
построить линию уровня x + y 2 x4 y=1 .
Преобразуем равенство:
x2+ y22 x4 y+1=0
( x22 x )+( y24 y )+1=0
( x22 x+1 )1+( y24 y+4 )4+1=0
( x1 )2+( y2 )2=4
( x1 )2+( y2 )2=22
Получили уравнение окружности с центром в точке O(1 ; 2 ) и радиусом R=2.
Сделаем чертеж:
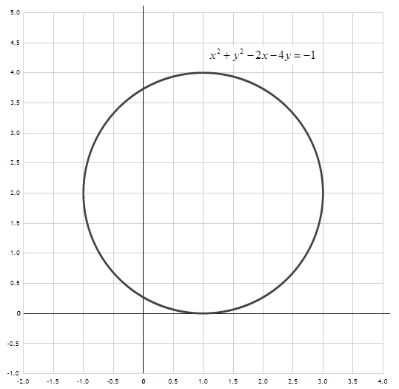
б) ...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
Р
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э