Решение задачи
Дана линейная оболочка L один R (альфа один, альфа два, альфа три, альфа четыре) . Выяснить, содержится ли линейная оболочка (табл. 5) в линейной оболочке
- Высшая математика
Условие:
Дана линейная оболочка 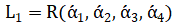 , где
, где  .
.
Выяснить, содержится ли линейная оболочка 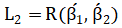 (табл. 5) в линейной оболочке
(табл. 5) в линейной оболочке 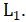
Табл. 5

Решение:
Для того, чтобы выяснить, содержится ли некоторая линейная оболочка в другой линейной оболочке достаточно показать, что все базисные вектора этой линейной оболочки являются линейно зависимыми от векторов этой другой оболочки, т.е. являются линейными комбинациями ее векторов.
Т.к. система векторов линейно независима между собой (векторы не коллинеарны: ) и очевидно полна в (любые вектора из - их линейные комбинации), то тогда они оба образуют базис линейной оболочки . Следовательно, необходимо проверить их линейную зависимость от векторов линейной оболочки
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
Р
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э