Дана матрица A линейного оператора в стандартном базисе трехмерного евклидова пространства. 1) Найти собственные значения и соответствующие им собственные подпространства данного оператора;
«Дана матрица A линейного оператора в стандартном базисе трехмерного евклидова пространства.
1) Найти собственные значения и соответствующие им собственные подпространства данного оператора;»
- Высшая математика
Условие:
Дана матрица A линейного оператора в стандартном базисе трехмерного евклидова пространства.
1) Найти собственные значения и соответствующие им собственные подпространства данного оператора;
2) Найти ортонормированный базис, состоящий из собственных векторов оператора;
3) Найти ортогональную матрицу T и диагональную матрицу B, для которой выполняется равенство 
4) Выяснить, имеет ли уравнение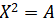 
решение в кольце матриц 
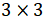над полем R.
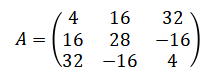
Решение:
1) Найдем собственные значения данного оператора.
Запишем характеристическое уравнение:
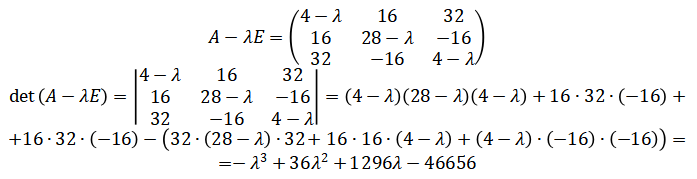
Решим найденное уравнение, чтобы найти собственные числа:
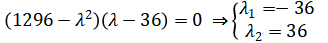
Следовательно, собственные значения это:
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э