Условие:
Дана невырожденная матрица A. Найти обратную матрицу A–1 и, пользуясь правилом умножения матриц, показать, что A · A–1 = E, где E – единичная матрица.
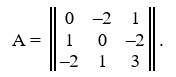
Решение:
Матрицей алгебраических дополнений B для данной квадратной матрицы A является матрица, полученная заменой каждого элемента матрицы A его алгебраическим дополнением.
Обратную матрицу A1 можно вычислить по следующей формуле:
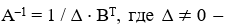определитель невырожденной матрицы A, BT транспонированная матрица B.
Вычисляем определитель матрицы A. Для этого предварительно вторую строку ...