Условие:
Дана система линейных уравнений. Доказать ее совместность и решить тремя способами:
1) по формулам Крамера;
2) методом Гаусса;
3) средствами матричного исчисления.
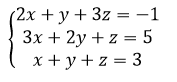
Решение:
Исследуем систему на совместность. Воспользуемся теоремой Кронекера-Капелли, для этого найдем ранг расширенной матрицы системы и ранг матрицы системы.
Найдем ранг матрицы методом элементарных преобразований. Ранг матрицы равен числу ненулевых строк в матрице после приведения её к ступенчатой форме при помощи элементарных преобразований над строками матрицы.

Ранг расширенной матрицы равен рангу матри...
