1. Главная
  2. Библиотека
  3. Высшая математика
  4. Дана выборка (объема 30) 1. Задать статистический ряд 2. Найти моду и медиану 3. Найти кумуляту относительных частот(выбор...

Дана выборка (объема 30) 1. Задать статистический ряд 2. Найти моду и медиану 3. Найти кумуляту относительных частот(выборочную функцию распределения) 4. На графике кумуляты отметить, как проекцию, медиану и верхний квартиль

«Дана выборка (объема 30) 1. Задать статистический ряд 2. Найти моду и медиану 3. Найти кумуляту относительных частот(выборочную функцию распределения) 4. На графике кумуляты отметить, как проекцию, медиану и верхний квартиль»
  • Высшая математика

Условие:

Дана выборка (объема 30) 

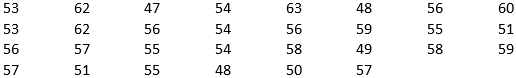
1.      Задать статистический ряд

2.      Найти моду и медиану

3.      Найти кумуляту относительных частот(выборочную функцию распределения)

4.      На графике кумуляты отметить, как проекцию, медиану и верхний квартиль

5.      Построить полигон частот

6.      Составить интервальный ряд,  взяв 7 интервалов.

7.      Построить гистограмму

8.      Ответить на вопрос: Можно ли по гистограмме сделать предположение о виде распределения генеральной совокупности.

9.      Найти числовые характеристики выборки:

среднее, дисперсию, исправленную выборочную дисперсию, выборочное среднее квадратическое отклонение и   исправленное выборочное среднее квадратическое отклонение.

Решение:

1.

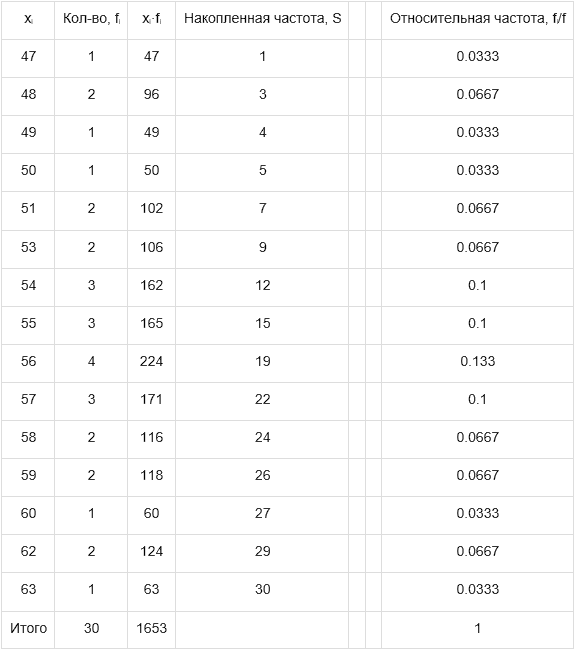
2.Мода.
Мода - наиболее часто встречающееся значение признака у единиц данной совокупности. мода равна 56.
Медиана.
Медианой (Me) называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности. Находим xi, при котором накопленная частота S будет больше f/2 = 16. Это значение xi = 56. Таким образом, медиана равна 56.

3. 4.

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я