Условие:
Даны вершины треугольника АВС
А (-8; 0) В (0; -6) С (4; 9)
Требуется найти:
1. длины сторон АВ и АС, их уравнения и угловые коэффициенты;
2. величину угла А в градусах; А (-8; 0), В (0; -6), С (4; 9)
3. уравнение биссектрисы АR угла А;
4. точку пересечения медиан треугольника АВС; А (-8; 0), В (0; -6), С (4; 9)
5. уравнение высоты CN и точку N её пересечения со стороной АВ;
6. уравнение прямой l, проходящей через вершину В параллельно стороне АС и её точку пересечения с высотой CN; А (-8; 0), В (0; -6), С (4; 9)
7. координаты точки D, симметричной точке С и лежащей на медиане СМ;
8. вычислить площадь четырехугольника АDBC. А (-8; 0), В (0; -6), С (4; 9), D (-12; -15).
Решение:
1. длины сторон АВ и АС, их уравнения и угловые коэффициенты;
Длины сторон АВ и АС определяем, как расстояние между двумя точками, используя соответствующую формулу:
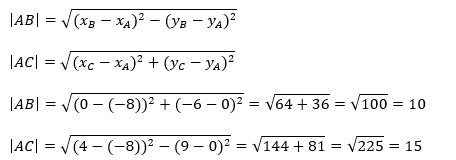
Составим уравнение прямой AС
Уравнение прямой, проходящей через две точки имеет вид:
