Условие задачи
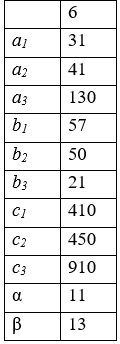
Для производства двух видов продукции А и В используются материалы трех сортов. На изготовление единицы изделия А (В) расходуется а1 (b1) кг материала 1-го сорта, а2 (b2) кг материала 2-го сорта, а3 (b3) кг материала 3-го сорта. Всего имеется с1, с2, с3 кг материалов 1-го сорта, 2-го сорта и 3-го сорта соответственно. Реализация единицы продукции А (В) приносит прибыль α (β) рублей. При каком объеме производства прибыть будет максимальна?
(первая строка таблицы – варианты с 1 по 10)
Ответ
Пусть продукции вида А необходимо выпускать х1, вида В х2, тогда ограничения по материалам:
1 сорт: 31x1+57x2410,
2 сорт: 41x1+50x2450,
3 сорт: 130x1+21x2910.
Т.к. количество продукции неотрицательно, то
x10,
x20.
Прибыль определяется как F=11x1+13x2, которую необходимо максимизировать.
Математическая модель имеет вид:
F = 11x1+13x2 max
31x1+57x2410,
41x1+50x2450,
130x1+21x2910,
x10,
x20.
Необходимо найти максимальное значение целевой функции
F = 11x1+13x2 max при системе ограничений:
31x1+57x2410, (1)41x1+50x2450, (2)130x1+21x2910, (3)x10, (4)x20, ...
