Условие задачи
Для случайной величины, заданной выборкой, с надежностью γ и уровнем значимости α, на отрезке [a, b ] (с числом разбиений отрезка, равным 10) и при неизвестном среднем квадратическом отклонении:
а) составить интервальный статистический ряд;
б) построить гистограмму относительных частот;
в) найти точечные и интервальные оценки математического ожидания и среднего квадратического отклонения;
г) проверить гипотезу о нормальном распределении по критерию согласия Пирсона.
Ответ
а) Построение интервального статистического ряда.
Определяем в ряду наблюдений (выборке) наименьшее и наибольшее значения признака: xmin и xmax.
Размах варьирования признака вычисляется по формуле: R = xmax - xmin.
В нашем случае: R = b - a.
Число интервалов (по условию): k = 10.
Длину частичного интервала определяем по формуле: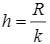 
Устанавливаем границы частичных интервалов. Так как по условию ...
