1. Главная
  2. Библиотека
  3. Высшая математика
  4. Для строительства пяти объектов используется кирпич, который изготавливают на трёх заводах. Ежедневно каждый из заводов мо...

Для строительства пяти объектов используется кирпич, который изготавливают на трёх заводах. Ежедневно каждый из заводов может изготовить: 110, 100, 90 усл. ед. кирпича.

«Для строительства пяти объектов используется кирпич, который изготавливают на трёх заводах. Ежедневно каждый из заводов может изготовить: 110, 100, 90 усл. ед. кирпича.»
  • Высшая математика

Условие:

Для строительства пяти объектов используется кирпич, который изготавливают на трёх заводах. Ежедневно каждый из заводов может изготовить: 110, 100, 90 усл. ед. кирпича. Ежедневные потребности в кирпиче на каждом из объектов соответственно составляют: 60, 90, 55, 45 и 50 усл. ед. Известны тарифы перевозок: 

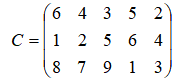
Необходимо составить математическую модель задачи и найти начальный план перевозок, используя методы: «северо-западного угла», минимального элемента, Фогеля. Найти оптимальный план транспортной задачи, используя метод потенциалов.

Решение:

Пусть xij - количество сырья, перевозимого от i-го поставщика j-му потребителю.

Параметры задачи это число поставщиков и потребителей, предложение и спрос сырья в каждом пункте, тарифы на перевозки. Ограничения задачи это ограничения на предложение и спрос сырья.

Критерием эффективности (целевой функцией) являются суммарные затраты S на перевозку, равные сумме произведений тарифов на перевозку на количество перевозимого сырья от каждого поставщика каждому потребителю.

Математическая модель задачи имеет вид:

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я