Для векторного поля а) проверить потенциальность; б) найти его потенциал .
«Для векторного поля а) проверить потенциальность; б) найти его потенциал .»
- Высшая математика
Условие:
Для векторного поля 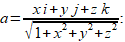
а) проверить потенциальность;
б) найти его потенциал 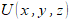 .
.
Решение:
а) Для потенциальности поля необходимо и достаточно, чтобы его ротор тождественно равнялся нулю. Проверяем, вычисляя ротор при помощи символического определителя:
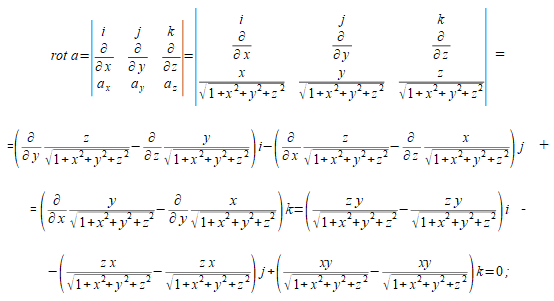
б) потенциальное поле является полем градиента некоторой скалярной функции , которая называется его потенциалом: Запишем это соотношение в координатной форме:
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э